소수를 찾는 방법은 고대 그리스의 수학자 에라토스테네스가 고안한 것으로, 소수를 체로 걸러 내는 것과 비슷하여 ‘에라토스테네스의 체’라고 합니다.
1에서 100까지의 소수를 찾아봅시다. 다음과 같은 방법으로 소수를 찾습니다.
① 1은 소수가 아니므로 1은 지웁니다.

② 2는 남기고 2의 배수들을 지웁니다.(일의 자리가 2,4,6,8,0으로 끝나는 많은 숫자들이 지워집니다.)

③ 3은 남기고 3의 배수들을 지웁니다.(지워져 있는 숫자들을 제외하고 9,15,21,27,33,39,45,51,57,63,69,75,81,87,93,99의 숫자가 지워집니다.)

4를 지울 차례라고 생각하는데 이미 지워져있습니다. 그래서
④ 5를 남기고 5의 배수들을 지웁니다.(25,35,55,65,85,95가 지워집니다.)

다시 6을 지울 차례인데 이미 6은 지워져있습니다. 그래서
⑤ 7은 남기고 7의 배수들을 지웁니다.(49,77,91이 지워집니다.)

이와 같은 방법으로 남은 수 중에서 처음 수는 남기고 그 수의 배수를 모두 지우면 됩니다.
⑥ 11을 남기고 11의 배수들을 지웁니다.(100까지의 숫자에는 더 이상 11의 배수가 존재하지 않습니다.)

⑦ 13을 남기고 13의 배수들을 지웁니다.(100까지의 숫자에는 더이상 13의 배수가 존재하지 않습니다.)

⑧ 17을 남기고 17의 배수들을 지웁니다.(100까지의 숫자에는 더이상 17의 배수가 존재하지 않습니다.)

⑨ 19를 남기고 19의 배수들을 지웁니다.(100까지의 숫자에는 더이상 19의 배수가 존재하지 않습니다.

⑩ 23을 남기고 23의 배수들을 지웁니다.(100까지의 숫자에는 더이상 23의 배수가 존재하지 않습니다.)
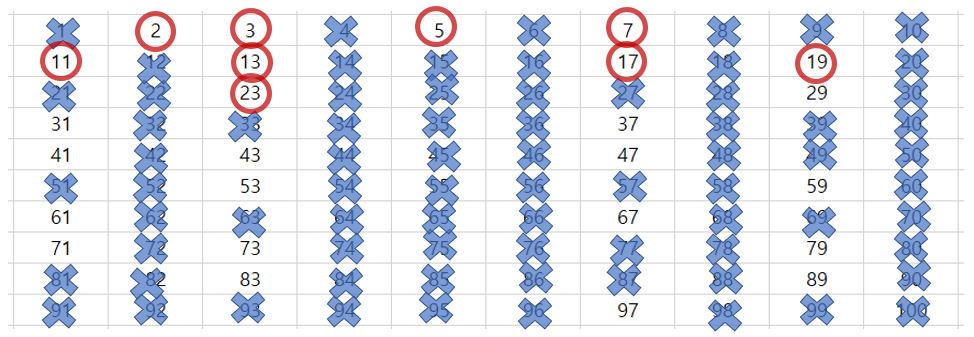
29를 남기고 29의 배수들을 지웁니다.(100까지의 숫자에는 더이상 29의 배수가 존재하지 않습니다.)

31를 남기고 31의 배수들을 지웁니다.(100까지의 숫자에는 더 이상 31의 배수가 존재하지 않습니다.)

37를 남기고 37의 배수들을 지웁니다.(100까지의 숫자에는 더 이상 37의 배수가 존재하지 않습니다.)

41를 남기고 41의 배수들을 지웁니다.(100까지의 숫자에는 더 이상 41의 배수가 존재하지 않습니다.)

43를 남기고 43의 배수들을 지웁니다.(100까지의 숫자에는 더 이상 43의 배수가 존재하지 않습니다.)

47를 남기고 47의 배수들을 지웁니다.(100까지의 숫자에는 더 이상 47의 배수가 존재하지 않습니다.)
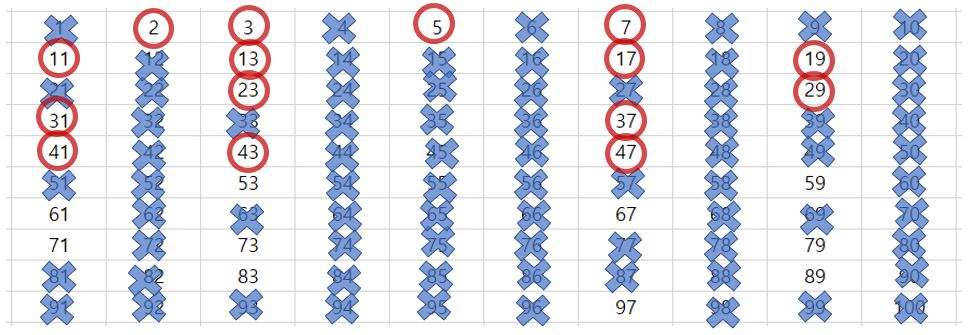
53를 남기고 53의 배수들을 지웁니다.(100까지의 숫자에는 더 이상 53의 배수가 존재하지 않습니다.)

50을 넘는 수들은 확인하지 않아도 알 수 있습니다. 그 이유는 2배를 하면 100을 넘기기 때문입니다.
그래서 이제는 남아있는 모든 수를 남기면 됩니다.

따라서 1부터 100까지의 소수는 2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97 입니다.
'중등 수학 > 중1 수학(1학기)' 카테고리의 다른 글
| [중1 수학] 소인수분해를 이용하여 최대공약수 구하는 방법 (0) | 2023.06.16 |
|---|---|
| [중1 수학] 최대공약수의 뜻, 서로소의 뜻, 최대공약수와 공약수의 관계 (0) | 2023.06.14 |
| [중1 수학] 소인수분해하는 방법(소인수,소인수분해, 제곱수의 뜻) (0) | 2023.06.13 |
| [중1 수학] 자연수의 분류(1, 소수, 합성수) 거듭제곱의 뜻 (0) | 2023.06.12 |
| [중1 수학] 소수를 왜 배우는가? (0) | 2023.06.10 |