- 순환소수의 뜻
Ⅰ. 유리수와 순환소수 1. 순환소수(2)
무한소수의 분류
앞글에서 유한소수와 무한소수에 대해서 알아보았다. (https://ksy3022.tistory.com/75)

이번에는 무한소수에 대해서 조금 더 깊게 생각해 보자. 유한소수는 더 깊게 생각할 것이 없다.
소수점 아래에 0이 아닌 숫자가 무한번 나오는 숫자들을 적어보자.

모두 무한소수이다. 이 무한소수들을 자세히 살펴보면 이것 또한 두 가지로 구분이 가능하다.
어떻게 나눌 수 있을까?
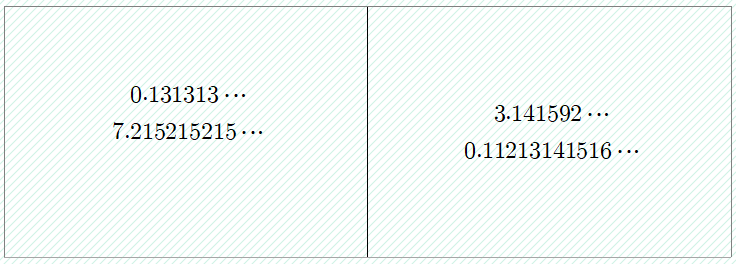
위와 같이 나눌 수 있다.
이렇게 나눈 기준은 무엇일까?

위와 같이
왼쪽의 무한소수들은 규칙적으로 같은 숫자가 반복됨을 알 수 있다.
오른쪽의 무한소수들은 규칙적으로 같은 숫자가 반복되지 않는다.
특히 오른쪽 아래의 숫자는 그 다음 숫자가 무엇이 나올지 알 수 있다. 나름 규칙이 있기 때문이다.
하지만 같은 숫자가 반복적으로 나오지는 않는다.
이들도 이러한 특징을 살펴서 이름 지어 주었다.
무엇이라고 지었을까?
감이 오는가? 같은 숫자가 반복적으로 돌고 돈다. (돌고 도는 것!! 과학시간에는 물의 순환을 배웠다.)
수학자들은
왼쪽의 무한소수들을 순환소수라고 이름 지어주었다.
순환소수의 뜻
순환소수의 뜻을 살펴보면 다음과 같다.

순환소수는 무한소수 중에서 규칙적으로 같은 숫자가 반복되는 것이다.
따라서, 소수점 아래에 일정한 숫자의 배열이 한없이 되풀이되는 것이다.
손환소수의 뜻에서 어떤 자리에서부터라는 표현은 무엇을 의미하는 것일까?
이 말은 소수점 아래의 첫번째 자리에서부터 같은 숫자가 규칙적으로 나와도 되고,
소수점 아래의 두 번째 잘에서부터 같은 숫자가 규칙적으로 나와도 된다는 말이다.
예를 들면 다음과 같다.

즉, 순환소수는 소수점 아래 첫 번째든 두 번째든 상관없이 일정한 숫자의 배열이 계속 반복적으로 나오는 무한소수를 뜻하는 것임을 알 수 있다.
여기서 잠깐!
순환마디

위의 표를 보면 숫자가 반복되는데 어떤 경우에는 3이 반복되고 어떤 경우는 17이 어떤 경우는 152가 반복됨을 알 수 있다.
그럼 이런 경우에
'소수점 아래에서 어떤 숫자들이 계속 반복되는가?'라고 질문을 해야 한다.
폼이 안 나고 너무 길다.
그래서 수학자들은 이것도 이름 지어 주었다.
무엇이라고 이름 지었을까?
순환마디이다!(하나의 마디가 계속 순환하니 순환마디라고 이름 붙여진 듯하다.)
순환마디의 정확한 뜻을 살펴보자.

순환마디가 순환소수에서 한없이 되풀이되는 부분이다. 그런데 가장 짧은 한 부분이라고 표현했을까?
다음 예를 살펴보자.

어느 말이 맞는 말일까?
가장 짧은 이라는 조건을 붙이지 않으면 둘 다 맞는 말이 된다.
수학자들은 왼쪽의 말만 옳다고 보기 위해서 가장 짧은 이라는 조건을 첨가했음을 알 수 있다.
다음 무한 소수들의 순환마디를 찾아보자.

순환마디를 찾으면 다음과 같다.

그러면 다음 무한소수의 순환마디를 찾아보자.

순환마디가 23일까? 13일까?
위의 무한소수의 순환마디는 13이다.
그 이유는 무엇일까?
순환마디의 뜻을 다시 살펴보자.

순환소수에서 소수점 아래에서 한없이 되풀이되는 가장 짧은 한 부분이다.
즉, 순환마디는 소수점 아래에서만 살펴본다는 뜻이다.
교과서에서 대부분은 다음과 같이 설명한다.

이때 한없이 되풀이되는 가장 짧은 한 부분을
소수점 아래라고 생각해야 한다는 것이다.
따라서, 아래의 숫자

은 소수점 아래에서만 보아야 하기 때문에 순환마디는 13이라고 하는 것이다.
'중등 수학 > 중2 수학(1학기)' 카테고리의 다른 글
| [중2 수학] 순환소수를 분수꼴로 나타내기(2) (0) | 2023.09.19 |
|---|---|
| [중2 수학] 분수를 보고 순환소수 알아내는 특별 비법 (0) | 2023.09.12 |
| [중2 수학] 분수를 보고 유한소수 알아내는 특별 비법 (0) | 2023.09.08 |
| [중2 수학] 순환소수 간단히 나타내기 (0) | 2023.09.05 |
| [중2 수학] 유한소수와 무한소수 (0) | 2023.08.29 |