- 사분면(제1사분면, 제2사분면, 제3사분면, 제4사분면)
Ⅳ. 좌표평면과 그래프 1. 순서쌍과 좌표(2)
좌표평면 4개의 영역으로 나누어진다!!
수직선위에 나타내지 못하는 점을 나타내기 위해서 세로선이 하나 더 필요했고
그래서 좌표평면이라는 게 생겨났다.
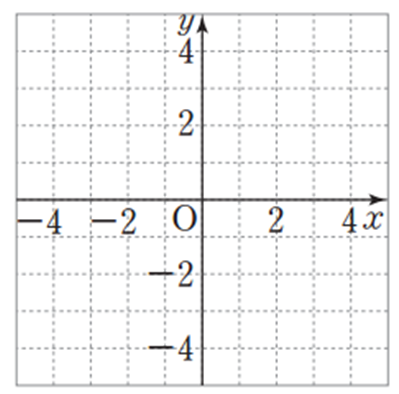
가로선과 세로선 즉, \(x\) 축과 \(y\)축에 의해서 좌표평면은 네 부분으로 나누어진다.
면이 4부분으로 나누어져서 이를 사분면이라고 부른다.
사분면의 이름 정하기
4 부분으로 나누어지는 각각의 명칭도 정하였다.
제1사분면, 제2사분면제, 3 사분면, 제4사분면
어느 곳을 제1사분면이라고 할까?
우리가 가장 편하게 느낄만한 곳이 1사분면이다.
우리는 가로선을 즉, \(x\) 축에 익숙해져 있다.
\(x\) 축을 기준으로 왼쪽보다는 오른쪽에 편안함을 느끼고,
\(x\)축을 기준으로 아래쪽보다는 위쪽에 편안함을 느낀다.
그곳이 제1사분면이 되는 것이다.
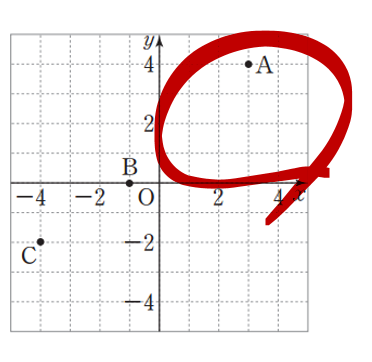
위의 표시된 영역을 제1사분면이라고 약속했다.
그러면 제2사분면은 어느 곳으로 정해야 할까?
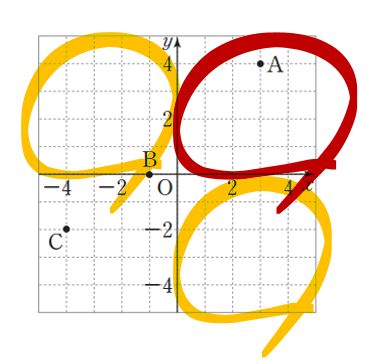
위의 그림처럼 제1사분면의 옆이나 아래 부분을 제2사분면으로 하면 적당할 듯하다.
그러면 두 곳 중 어느 곳이 편하게 느껴지는가?
\(x\) 축의 아래쪽보다는 위쪽이 편하다.
따라서, 아래 그림처럼 제2사분면의 위치를 정하게 되었다.
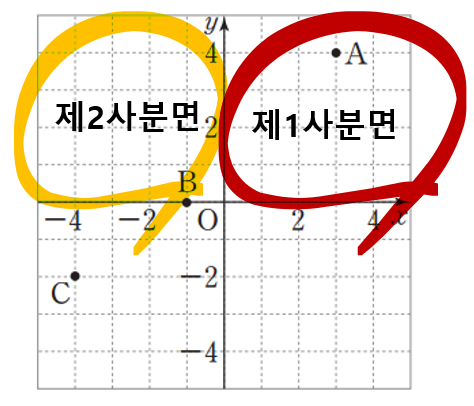
그러면 이제 제3사분면의 위치를 정해야겠다.
남은 두 곳 중에서 어느 곳을 제3사분면이라고 해야 할까?
여기에서는 어느 곳이 편안함을 느끼는가 보다는 규칙을 적용하였다.
지금 제1사분면과 제2사분면의 위치를 정했으니 그 규칙에 의해서 제3사분면의 위치를 정했다.
지금 시계 반대방향으로 가고 있어서 시계 반대방향에 위치한 곳을 제3사분면, 그다음을 제4사분면이라고 정했다.

이를 정리하면 다음과 같이 나타낼 수 있다.
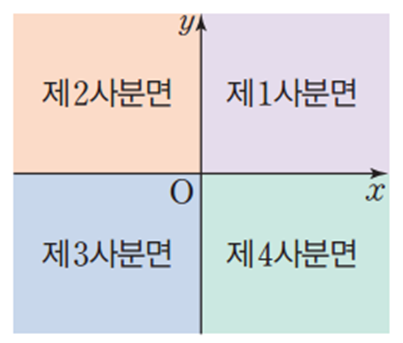
* 좌표축 위의 점은 어느 사분면에도 포함되지 않는다!!
사분면에 따른 좌표의 부호
점 \(P(a, b)\)의 위치에 따라서 \(a\)와 \(b\)의 부호를 다음과 같이 나타낼 수 있다.
 |
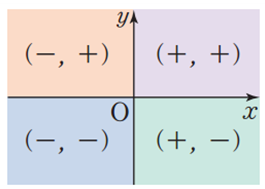 |
'중등 수학 > 중1 수학(1학기)' 카테고리의 다른 글
| [중1 수학] 정비례 관계 (0) | 2023.08.08 |
|---|---|
| [중1 수학] 그래프란? (0) | 2023.08.04 |
| [중1 수학] 순서쌍과 좌표평면 (0) | 2023.07.30 |
| [중1 수학] <3단원 문자와 식> 정리 (0) | 2023.07.29 |
| [중1 수학] 복잡한 일차방정식의 풀이(거리, 속력, 시간에 관한 문제) (0) | 2023.07.28 |