- 일차식과 수의 곱셈
- 일차식과 수의 나눗셈
2. 일차식과 수의 곱셈, 나눗셈(2)
식을 이루는 각각의 항을 하나의 수와 같이 생각할 수 있다. 문자도 곱해져 있을 뿐 유리수의 사칙계산과 같은 방법이다.
우선 일차식의 종류를 크게 두 가지로 나누어 생각해 보자.
단항식과 다항식으로 나누어 구분할 수 있다.
일차식 중에서 단항식은 \(5x, -2y\)와 같은 것이 있고,
다항식은 \(5x-2y, 5x+1, x+y-1\)과 같은 것이 있다.
그러므로 일차식과 수의 곱셈을 두 가지로 구분하여 생각해 보자.(도형과 식으로 각각 살펴보자.)
(1) (단항식) × (수) 또는 (수) × (단항식)
예를 들어 \(5x\)×\(3\)을 살펴보자.
① 작은 직사각형의 넓이는 \(5x\)이고 같은 크기가 \(3\)개가 있으므로 이를 식으로 표현하면 \(5x\)×\(3\)으로 나타낼 수 있다.
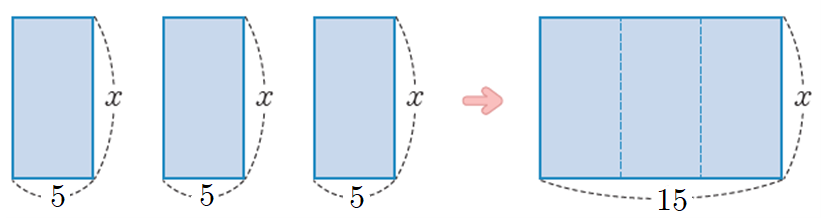
위의 그림에서 작은 직사각형의 넓이의 합은 전체 직사각형의 넓이의 합과 같아서
가로의 길이는 \(15\)가 되고 세로의 길이가 \(x\)이므로 직사각형의 넓이는 \(15x\)임을 알 수 있다.
즉, \(5x\)×\(3=15x\) 이다.
② 이번에는 식으로 살펴보자.
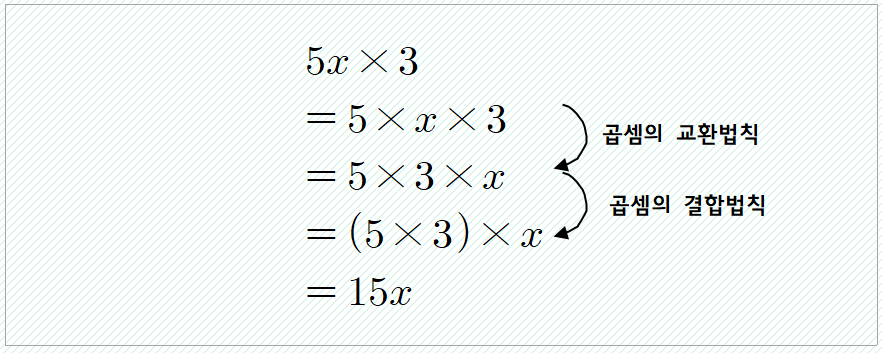
➜ 곱셈의 교환법칙과 결합법칙을 이용하여 수끼리 먼저 곱한 후 문자 앞에 쓴다.
(2) (다항식)×(수) 또는 (수)×(다항식)
예를 들어 \(7(2x+3y)\)를 살펴보자.
큰 직사각형의 넓이는 가로가 \(2x+3y\) 이고, 세로가 \(7\)이므로 이를 곱한 \(7(2x+3y)\)로 나타낼 수 있다.
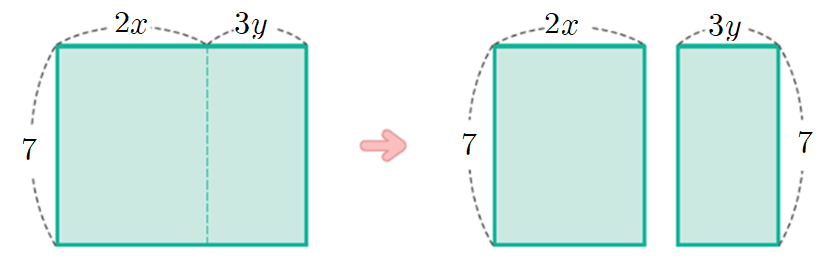
위의 그림처럼 큰 직사각형을 작은 직사각형으로 쪼개면
가로의 길이가 \(2x\)이고 세로가 \(7\)인 직사각형과 가로의 길이가 \(3y\)이고 세로가 \(7\)인 직사각형으로 나눌 수 있다.
각각의 넓이는 \(2x\) × \(7\)과 \(3y\) × \(7\) 이 된다.
이를 식으로 나타내보면 다음과 같이 나타낼 수 있다.
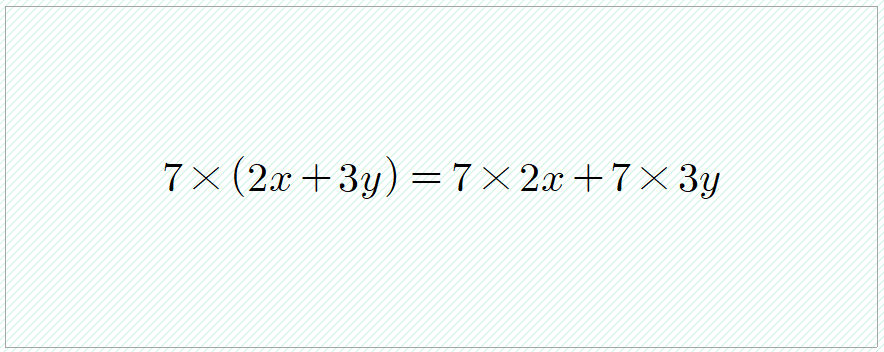
즉, 분배법칙이 성립함을 알 수 있다.
➜ 분배법칙을 이용하여 일차식의 각 항에 수를 곱하여 계산한다.
'중등 수학 > 중1 수학(1학기)' 카테고리의 다른 글
| [중1 수학] 동류항의 뜻, 동류항의 덧셈과 뺄셈하는 방법 (0) | 2023.07.18 |
|---|---|
| [중1 수학] 일차식과 수의 나눗셈 계산 (0) | 2023.07.17 |
| [중1 수학] 다항식에서 사용하는 용어 살펴보기(차수, 계수, 항, 상수항 등) (0) | 2023.07.15 |
| [중1 수학] 대입의 뜻, 식의 값 구할 때 주의사항 (0) | 2023.07.14 |
| [중1 수학] 문자를 사용해서 식 간단히 나타내기(곱셈 기호 ×, 나눗셈 기호 ÷의 생략) (0) | 2023.07.13 |