반응형
- 정수와 유리수의 곱셈
5. 정수와 유리수의 곱셈(1)
덧셈과 곱셈의 관계

같은 수를 여러 번 더했을 때, 이를 간단히 나타내기 위해 곱셈으로 바꿔서 나타낼 수 있다.
즉, 곱셈은 다음과 같이 덧셈으로 바꾸어 나타낼 수 있음을 기억하자.
2×5 : 2를 5번 더한 것이므로 다음과 같이 나타낼 수 있다.

정수의 곱셈을 다음과 같이 4가지 경우로 나누어 생각해 보자.
(양수) ×(양수),
(양수) ×(양수), (음수) ×(양수)의
곱셈을 덧셈으로 바꾸어 생각해 보면
(양수) ×(양수)
(음수) ×(양수)


이를 정리해 보자.

숫자끼리의 곱이라는 표현이 고급스럽진 않다.
수학적 용어를 사용해서 나타낼 수는 없을까?
숫자끼리의 곱을 절댓값의 곱으로 표현하면 적절하다.
따라서 위의 표를 다음과 같이 간단히 나타낼 수 있다.
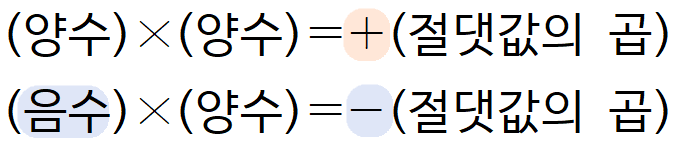
(양수) ×(음수), (음수) ×(음수)의 계산
곱하는 수가 음수인 경우에는 위의 경우처럼 적용할 수가 없다.
(음수)를 곱했을 때, 음수번 더하는 것에 대해서 논의한 적은 없다.
위의 (양수) ×(양수), (음수) ×(양수)를


이를 정리해 보자.

숫자끼리의 곱을 절댓값이라는 용어로 바꾸면 다음과 같이 나타낼 수 있다.

반응형
'중등 수학 > 중1 수학(1학기)' 카테고리의 다른 글
| [중1 수학] 곱셈과 나눗셈의 관계, 정수와 유리수의 나눗셈 (0) | 2023.07.06 |
|---|---|
| [중1 수학] 곱셈의 교환법칙과 결합법칙 (0) | 2023.07.05 |
| [중1 수학] 덧셈과 뺄셈의 혼합 계산 (0) | 2023.07.03 |
| [중1 수학] 덧셈과 뺄셈의 관계 이해하기 (0) | 2023.07.02 |
| [중1 수학] 덧셈의 교환법칙, 결합법칙 (0) | 2023.07.01 |