- 반비례를 표, 식, 그래프로 나타내기
Ⅳ. 좌표평면과 그래프 4. 반비례(2)
반비례 그래프는 어떻게 그리나?
반비례 그래프 \(y=a/x\) (단, \(a>0\))에 대해서 살펴보자.
우선 \(y=6/x\)의 그래프를 그려보자.
\(x\)와 \(y\) 사이의 관계를 생각하여 다음 표를 채워보자.

\(x\)와 \(y\) 사이의 관계를 표로 나타내면 다음과 같다.

위의 표에서 \(x\)의 값을 \(x\) 좌표의 값을 \(y\) 좌표로 하는 순서쌍 \((x, y)\)를 좌표로 하는 점으로 나타내 보자.
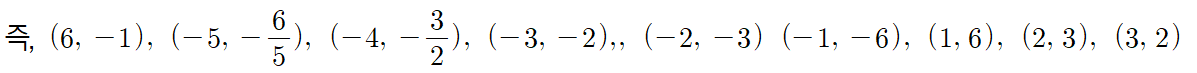
위의 순서쌍을 좌표평면 위에 나타내어 보자.
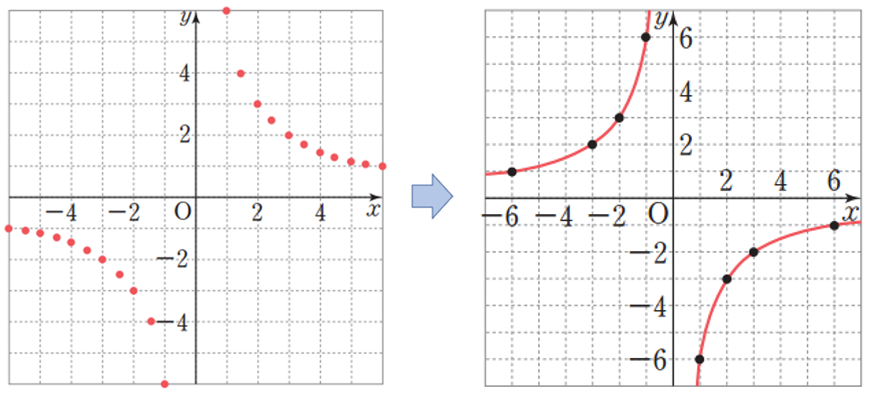
\(x\)의 값의 간격을 좀 더 촘촘히 하여 더 많은 순서쌍을 만든 후 이를 좌표로 하는 모든 점을 좌표평면 위에 나타내면 다음과 같이 그래프의 모양은 한없이 뻗어 나가는 한 쌍의 매끄러운 곡선이 된다.

위와 같은 방법으로 반비례 관계 \(y=a/x\) (단, \(a>0\))의 꼴의 그래프를 여러 개 그려보면
모두 원점에 대하여 대칭이고 좌표축에 한없이 가까워지는 한 쌍의 매끄러운 곡선이 됨을 확인할 수 있다.
반비례 그래프 \(y=a/x\) (단, \(a>0\))
반비례 \(y=a/x\) (단, \(a>0\))
① \(x=0\) 의 값은 존재하지 않는다.
② \((1, a)\)를 지난다.
③ 제1사분면, 제3사분면을 지난다.
④ \(x\)의 값이 증가하면 \(y\)의 값도 증가한다.
반비례 그래프 \(y=a/x\) (단, \(a <0\))
이번에는 반비례 그래프 \(y=a/x\) (단, \(a <0\))에 대해서 살펴보자.
\(y=-6/x\)의 그래프를 그려보자..
\(x\)와 \(y\) 사이의 관계를 표로 나타내면 다음과 같다.

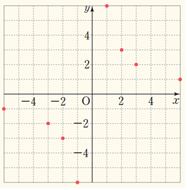
위의 표에서 얻어지는 순서쌍 \((-6, 1)\),\((-3, 2)\),\((-2, 3)\),\((-1, -6)\),\((1, -6)\),\((2, -3)\),\((3, -2)\),,\((6, -1)\)를 좌표로 하는 점을 좌표평면 위에 나타내면 다음그림의 점들이 된다.
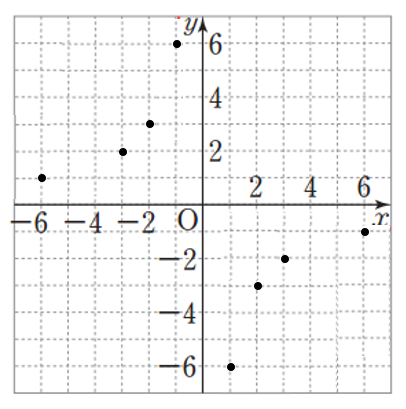
\(x\)의 값의 간격을 좀 더 촘촘히 하여 더 많은 순서쌍을 만든 후 이를 좌표로 하는 모든 점을 좌표평면 위에 나타내면 다음과 같이 그래프의 모양은 점점 직선에 가까워지게 된다.
위와 같은 방법으로 반비례 관계 \(y=a/x\) (단, \(a <0\))
모두 원점에 대하여 대칭이고 좌표축에 한없이 가까워지는 한 쌍의 매끄러운 곡선이 됨을 확인할 수 있다.
여기에서 위에 나왔던 그래프 모양과 차이점이 생긴다는 것을 알게 된다.
반비례 그래프 \(y=a/x\) (단, \(a <0\))
반비례 \(y=a/x\) (단, \(a <0\))의 그래프의 특징을 살펴보자.
① \(x=0\) 의 값은 존재하지 않는다.
② \((1, a)\)를 지난다.
③ 제2사분면, 제4사분면을 지난다.
④ \(x\)의 값이 증가하면 \(y\)의 값은 감소한다.
반비례 그래프 쉽게 그리는 방법??
어떤 방법으로 그리면 반비례 그래프를 쉽게 그릴 수 있을까?
반비례 \(y=a/x\) (단, \(a≠0\)) 그래프의 특징을 살펴보자.
① \(x=0\) 의 값은 존재하지 않는다.
② \((1, a)\)를 지난다.
③ 모두 원점에 대하여 대칭이고 좌표축에 한없이 가까워지는 한 쌍의 매끄러운 곡선이다.
제1사분면에 그려지면 제3사분면에 그려지고,
제2사분면에 그려지면 제4사분면에 그려진다.
반비례 그래프는 정비례 그래프만큼 쉽게 그릴 수 있는 방법이 없다.
\(x\) 좌표와 \(y\) 좌표가 모두 정수인 순서쌍을 찾아 좌표평면에 점을 찍은 후 매끄럽게 곡선으로 연결하면 그나마 쉽게 그린 것이라 할 수 있다.
'중등 수학 > 중1 수학(1학기)' 카테고리의 다른 글
| [중1 수학] <4단원 좌표평면과 그래프> 정리 (0) | 2023.08.22 |
|---|---|
| [중1 수학] 반비례 관계 (0) | 2023.08.15 |
| [중1 수학] 정비례 관계의 그래프 (0) | 2023.08.11 |
| [중1 수학] 정비례 관계 (0) | 2023.08.08 |
| [중1 수학] 그래프란? (0) | 2023.08.04 |